1. The Ubiquity of $\pi$
or, Life, the Universe, and Everything: A Simple Statement of Fact
$\pi$ is everywhere you look. It is even the case that there is $\pi$ in the sky. We need $\pi$ in order to live and function. These three observations are fundamental to the way our universe is put together.
2. The Value of $\pi$
or, How Much is that Round Thing in the Window?
(with apologies to Patti Page) So, for fun, let’s calculate $\pi$ using Ramanujan’s famous infinite series formula, and check the error against a clever, arbitrary-precision algorithm for $\pi$, based on the Chudnovsky brothers’ improvement on Ramanujan’s series approximation, and which is correct to as many digits as we care to specify. While we’re at it, we’ll include just a straight-up implementation of the Chudnovsky brothers’ series approximation, too.
Ramanujan’s formula (see also here, and here):
\begin{equation}
\dfrac{1}{\pi} = \dfrac{2\sqrt 2}{9801}
\sum_{n=0}^{\infty} \dfrac{\left(4 n\right)!}{\left(n!\right)^4}
\dfrac{1103 + 26390\,n}{396^{4n}} \label{eq:ram}
\end{equation}
As mentioned here, the Chudnovsky brothers derived a Ramanujan-like formula that converges considerably faster(!) than Ramanujan’s original:
\begin{equation}
\dfrac{1}{\pi} = \dfrac{1}{53360\sqrt{640320}}
\sum_{n=0}^{\infty} \left(-1\right)^n
\dfrac{\left(6 n\right)!}{\left(n!\right)^3\left(3 n\right)!}
\dfrac{13591409 + 545140134\,n}{640320^{3n}} \label{eq:chud}
\end{equation}
We can take advantage of Python’s decimal module for exact arithmetic to as many digits of precision as we might want in calculating each term of the series. Doing so, we find the following errors after each successive iteration of the two series (note the exponents!):
Ramanujan Chudnovsky
n Rpi(n)-pi Cpi(n)-pi
-- ---------- -----------
0 7.642E-8 -5.903E-14
1 6.395E-16 3.078E-28
2 5.682E-24 -1.721E-42
3 5.239E-32 1E-56
4 4.944E-40 -5.959E-71
5 4.741E-48 3.609E-85
6 4.599E-56 -2.212E-99
7 4.5E-64 1.368E-113
8 4.433E-72 -8.515E-128
9 4.391E-80 5.331E-142
10 4.37E-88 -3.353E-156
11 4.364E-96 2.117E-170
12 4.372E-104 -1.341E-184
13 4.393E-112 8.513E-199
14 4.424E-120 -5.42E-213
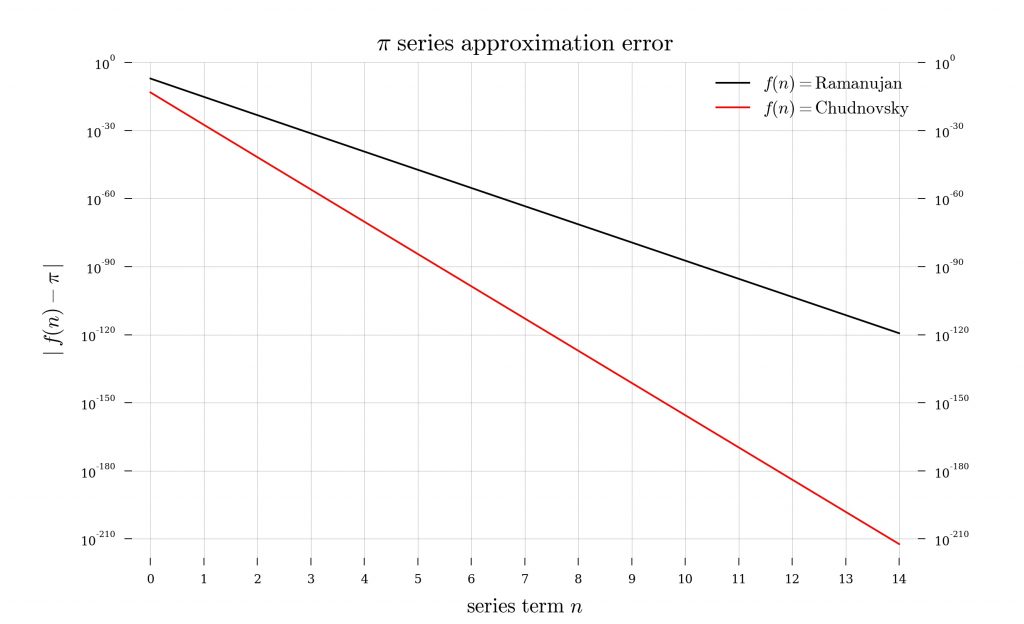
As we can see, Ramanujan’s formula, eq. \eqref{eq:ram}, gives eight orders of improvement (i.e., eight more digits of accuracy) per successive iteration, while the Chudnovsky formula, eq. \eqref{eq:chud}, yields fourteen orders of precision per iteration!
To illustrate, after fifteen Chudnovsky series terms, the difference between the series approximation and the actual value of $\pi$ is:
-0.00000 00000 00000 00000 00000 00000 00000 00000 00000 00000
00000 00000 00000 00000 00000 00000 00000 00000 00000 00000
00000 00000 00000 00000 00000 00000 00000 00000 00000 00000
00000 00000 00000 00000 00000 00000 00000 00000 00000 00000
00000 00000 00542...
Even just the first Chudnovsky term by itself (or just the first two Ramanujan terms) gives $\pi$ to almost machine precision ($2^{-52}\approx 2.22\!\times\!10^{-16}$) on a 64-bit computer.
For another perspective (thanks for the idea, Daniel Greenspan), let’s calculate (roughly!) the total number of atoms in the universe. As you might imagine, this will be a big number. We’ll break it down into two parts.
First, how many stars are in the universe? This is a number we can estimate from observations of galaxies and the amount of light that they emit. Essentially, since we can determine distances to galaxies, we just add it all up. Modern astronomical estimates for the equivalent number of solar-mass stars in our universe, based on the amount of light we detect coupled with the distances to the objects (galaxies) emitting that light, all come in at around
\begin{equation}
N_{stars} \approx 2\!\times\!10^{23} \label{eq:Nstars}
\end{equation}
This is equivalent to the mass of the visible universe divided by the mass of the Sun.
The amount of baryonic—that is, visible, or what we think of as “normal”—matter in the universe is only a small fraction of the total mass of the universe. Our universe, based on several different kinds of observations, is $68.3\%$ dark energy, $26.8\%$ dark matter, and $4.9\%$ ordinary matter. But that’s another story. We’ll just stick to the ordinary matter that we can detect via the electromagnetic radiation it emits.
Second, how many atoms are in a star the mass of our Sun? Now, the Sun has a measured mass of $M_{\odot} = 1.9884\!\times\!10^{30}$kg(†) and is composed of about $74.9\%$ hydrogen and $23.8\%$ helium by mass(‡). For this exercise, we will assume that the mass contributions of electrons and the other elements besides hydrogen and helium are negligible. The mass of a proton is $1.00784$amu, and the mass of a helium nucleus is $4.002602$amu. One amu (atomic mass unit) is $1.66053904\!\times\!10^{-27}$kg. The approximate number of atoms in the Sun, $N_{\odot}$, is then
\begin{equation}
N_{\odot} \approx
\dfrac{0.749 M_{\odot}}{1.00784\mathrm{amu}} +
\dfrac{0.238 M_{\odot}}{4.002602\mathrm{amu}}
\approx 9.6 \!\times\!10^{56} \mathrm{atoms} \label{eq:Nsuns}
\end{equation}
Hence, combining \eqref{eq:Nstars} and \eqref{eq:Nsuns}, the number of atoms in the universe, $N_{universe}$, is, roughly,
\begin{equation}
N_{universe} \approx N_{stars}\cdot N_{\odot}
\approx 1.9\!\times\!10^{80} \mathrm{atoms}
\end{equation}
Notice from the table above that the error of the Chudnovsky series after only the first six terms is about one part in $2.8\!\times\!10^{84}$—a number that is several orders of magnitude larger than the number of atoms in the entire universe!
3. A Short Introduction to Astrophysics
or, Is there Really $\pi$ in the Sky?
or, Here are the Footnotes
You might not have seen this coming. But here it is, wherein we demonstrate that, indeed, there is $\pi$ in the sky.
(†) We can determine the mass of the Sun by measuring the motions of the planets and asteroids in our Solar System, and then using Newton’s Law of Gravity. As Kepler discovered from Tycho Brahe’s meticulous observations, and Newton proved mathematically after he invented calculus and then turned his attention to the Moon’s motion, the orbital period $P$ of a body of mass $m$ and its mean distance $a$ from the Sun with mass $M_{\odot}$ are related by
\begin{equation}
P^2 = \dfrac{4 {\pi}^2}{G\left(M_{\odot}+m\right)} a^3
\end{equation}
Look at that: $\pi$ is in this equation that describes what we see in the sky.
(‡) We can determine the relative abundances of the elements that make up the Sun (and almost any star) by measuring, with a spectroscope, the amount of radiation absorbed by those elements in the atmosphere of the Sun (called the photosphere). Every element has its own discrete spectral signature in the form of absorption lines at specific sets of wavelengths. The amount of radiation absorbed by an element, relative to the other elements present, and in combination with the measured temperature, luminosity, and mass of a star, tells us what fraction of the star’s photosphere consists of that element. (We also need to know the distance to the star, but that’s a long story.)
Stars are, roughly speaking (i.e., ignoring the radiation absorbed by the elements in their photospheres), black body radiators. This means we can relate their luminosity (total radiated energy per unit time) to their radius $R$ and their effective surface temperature, $T_{eff}$. Simply put, the luminosity is the surface area of the star ($4\pi R^2$) times the amount of radiation emitted per unit surface area of the star:
\begin{equation}
L = 4\pi R^2 \sigma T_{eff}^4 \label{eq:L}
\end{equation}
where $\sigma = \dfrac{2\pi^5 k^4}{15 c^2 h^3}$ is the Stefan-Boltzmann constant, $k=1.38064852\!\times\!10^{−23}$ Joules per degree Kelvin ($J\cdot K^{-1}$) is the Boltzmann constant, $c$ is the speed of light in vacuum, and $h=6.62607015\!\times\!10^{−34} J\cdot s$ is the Planck constant from quantum mechanics. Eq. \eqref{eq:L} is a consequence of the physics of black body radiation.
Look at that: $\pi$ is integral to these relations that describe what we see in the sky, too.
(Don’t ask about the quantum mechanics connection. You can go down that rabbit hole by following the provided links. Quantum mechanics hurts my head.)
4. Full Disclosure
or, So This is Where That Came From
The Python code that produces the Ramanujan and Chudnovsky results (table and plot) is:
import decimal
from decimal import Decimal as D
from utils import mutils
from utils import mplot as plt
prec = 300 # Set the number of digits of precision
# for calculations.
decimal.getcontext().prec = prec
def dfac(n):
""" Arbitrary digits factorial. """
m = D('1')
for k in range(1,n+1):
m *= k
return m
def Rpi(n):
"""
Calculate pi using n iterations of Ramanujan's
formula.
"""
s = D('0')
for k in range(n+1):
facterm = dfac(4*k)/dfac(k)**4
num = D('1103') + D('26390')*k
den = D('396')**(4*k)
s += facterm*num/den
s *= D('8').sqrt()/D('9801')
return 1/s
def Cpi(n):
"""
Calculate pi using n iterations of the Chudnovsky
brothers' Ramanujan-like formula.
"""
s = D('0')
for k in range(n+1):
facterm = dfac(6*k)/(dfac(k)**3*dfac(3*k))
num = D('13591409') + D('545140134')*k
den = D('640320')**(3*k)
s += D('-1')**k*facterm*num/den
s *= D('1')/(D('53360')*D('640320').sqrt())
return 1/s
# Print a table of the error of n iterations
# of Ramanujan's formula.
print(' Ramanujan Chudnovsky')
print(' n Rpi(n)-pi Cpi(n)-pi')
print('-- ---------- -----------')
fmt = '{:2d} {:>10s} {:>11s}'
c4 = decimal.Context(prec=4)
rerrs = []
cerrs = []
for n in range(15):
exact_pi = D(mutils.pi_chudnovsky(prec))
errR = Rpi(n) - exact_pi*D('1e-{:d}'.format(prec))
errC = Cpi(n) - exact_pi*D('1e-{:d}'.format(prec))
normerrR = errR.normalize(c4)
normerrC = errC.normalize(c4)
print(fmt.format(n, str(normerrR), str(normerrC)))
rerrs.append(float(errR))
cerrs.append(float(errC))
fig = plt.figure(figsize=(8.2, 5))
xlab = ['$\mathrm{number\ of\ series\ terms}\ n$', 12]
ylab = ['$\mid f(n) - \pi \mid$', 12]
pt = ['$\mathrm{\pi\ series\ approximation\ error}$',
14]
labs = [['$f(n) = \mathrm{Ramanujan}$', 10],
'$f(n) = \mathrm{Chudnovsky}$']
xticks = np.arange(15)
yticks = np.array([0.1**k for k in range(0, 240, 30)])
ylim = (1e-220, 1e-1)
plt.lineplot([np.array(rerrs), abs(np.array(cerrs))],
np.arange(15), ['k-', 'r-'], [1, 1],
ylim=ylim, logy=True, xlab=xlab,
ylab=ylab, xticks=xticks, yticks=yticks,
doxticks='bottom', doyticklabels='both',
dolegend=True, labels=labs, plottitle=pt)
fname = (os.environ['PYTHONPATH'] +
'/misc/Ramanujan pi.jpg')
plt.savefig(fname, dpi=300)

Having fun on Pi day? Oh yes!
from lat. manus – “hand” and scribo – “I write”) [1]