Aperiodic Wanderings

The evening looks promising.

Transparent air, crystalline blue—emblematic of Flagstaff even in summer—has soothed my soul since childhood. “I can see for miles and miles…” spins in my head, unbidden, as I walk a short patch of worn asphalt, dull gray and pitted from winter’s attacks. Dark green Ponderosa forest broods to the horizon, turning black as the light dims and the usefulness of my retinal color sensors fades. Thin, dry air is a poor thermal insulator, so it chills rapidly after sunset. I zip my jacket.

Ritual scan of the sky, projecting ahead several hours: gauging the night’s weather and observing conditions is an habitual game. I occasionally misjudge, but not tonight. The door clacks shut behind me. I know my keys are in my pocket, but I check anyway. I aim toward the chipped, institutional-turquoise railing in front of the dome. Cirrus lie low in the southwest, painted grunge by twilight and distance (thirty, forty miles). These will likely keep to their remove and not interfere. I pretend to decree it so.

As I shuffle southwest, my face parts the breeze. My felt hat stays on my head, unassisted. I’ve no need to glance at our rooftop weather station’s wind vane or anemometer. It should be a good night, the air clinging to the forest laid out before me as it flows, laminar and unturbulent, lifting with the ridge upon which we root and gliding smoothly overhead. Trudy, our night observer, should get one arcsecond seeing at the 61-inch telescope, perched on its massive concrete pedestal three stories up. It is the world’s most precise star measuring engine. Down here at the parking lot, the air will be more agitated. I’ll see two arcseconds, maybe a bit less, at the 51-inch telescope which squats inside a dome off the edge of the cooling asphalt. The dome resembles R2D2 from Star Wars.

“Seeing” is astronomer jargon for what our roiling atmosphere does to starlight, pushing and shoving it, forcing it to wiggle erratically in random directions as cells of turbulent air, refractive indexes varying slightly from their neighbors, scurry across our line of sight. These pockets of air, fleeing distant large-scale atmospheric pressure gradients, attest to forces at work beyond our tiny purview. This is why stars twinkle.

Baleful blood-red Scorpion heart, Antares, sits low in the south. The orb flashes sharp red and green and yellow and blue (if you stare carefully), dancing. Astronomers hate that. Twinkling harbingers fuzzed, mushy, corpulent images. Spica is higher in the sky, its hard, white-blue light passing through less of our atmosphere. It holds fairly steady, only an occasional flicker. I look higher. Orangey Arcturus, one of my favorite stars, stares unblinking, steady, solid. Some part of my brain registers that stars higher than about forty degrees above the horizon will be sharp tonight. I notice muscles relaxing, a growing anxiety over data quality now dissipates. Mona Lisa smile: in this clear air, the night will be dark and the Milky Way will billow, almost flocculent, and span the entire vault of the sky. I will remember later to emerge and gape at this wonder until my neck aches. Da Vinci would understand.

models fitted to a star’s intensity profile (click to enlarge)

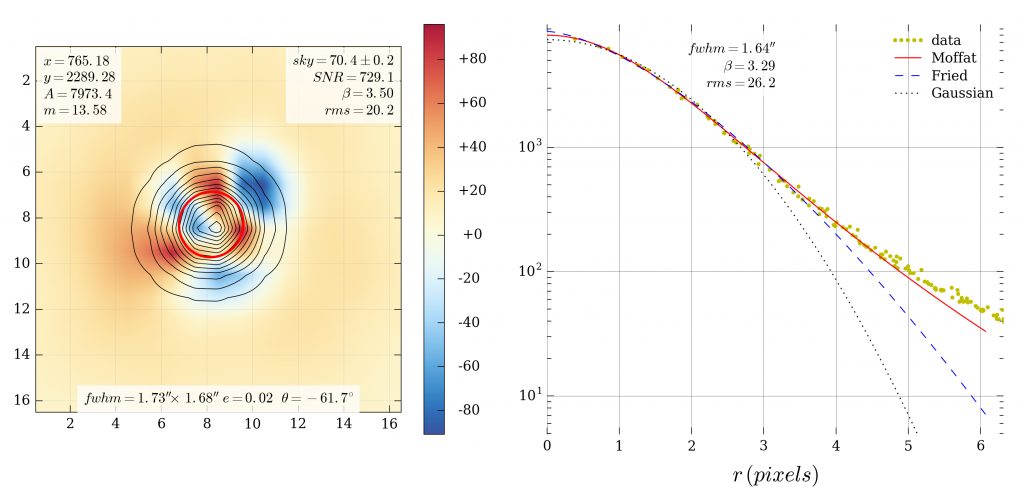
Scientists quantify. Astronomers’ measure of seeing—our means of taking the guesswork out of comparing one night to another—is the size of a star’s disk at the focal point of a telescope (that is, on the sensor hanging off its butt end). The width of a circle drawn half-way down from the central, brightest point of the disk that is a star image to its edge as it merges into the sky background is that measure. We call it “full width, half max”, or FWHM.

We measure angles with telescopes—immense, expensive protractors. This star is so many fractions of a degree from that star. A sixtieth of a degree is an arcminute. Your eyes can resolve details down to about one arcminute, or slightly less. A sixtieth of an arcminute is an arcsecond. An arcsecond is a very small angle: the apparent size of a U.S. quarter, 3.1 miles away. (The 61-inch telescope can measure angles to within one thousandth of an arcsecond.) “Good” seeing is when the FWHM of a star image is one arcsecond or less—a useful cultural agreement. Three arcseconds is bad. Five is horrendous, and the stars are dancing madly, taunting and useless, all the way to the zenith.

Inside the dome, chill seeps through my clothes as I wait for dome shutters and mirror covers to open the telescope’s eye to the heavens. As the liquid nitrogen tank satiates the camera dewar in pulsing spurts, a valve trips and vents excess pressure; the hiss is painful. I escape into the side room and toggle switches, powering various devices. The air compressor initiates a new aural assault. I plug my ears. Why did it choose now, I think. Several of us conjecture that the 51-inch telescope is inhabited by gremlins, not so much malevolent as impish, irritating. Maybe they are leprechauns. Back in the dome, motors stop and the nitrogen tank has finished its rhythmic regurgitation of cold. Pulling on insulated blue gloves meant for such things, I disconnect and stow the thick umbilical hose, its business end caked with ice, thin sheets of condensing air flowing to the dome floor. The drive motors wake and hum, a happy sound, as I feed them power. Everything inside this dome is thirsty.

We are ready for the night.

the 51-inch telescope (click to enlarge)